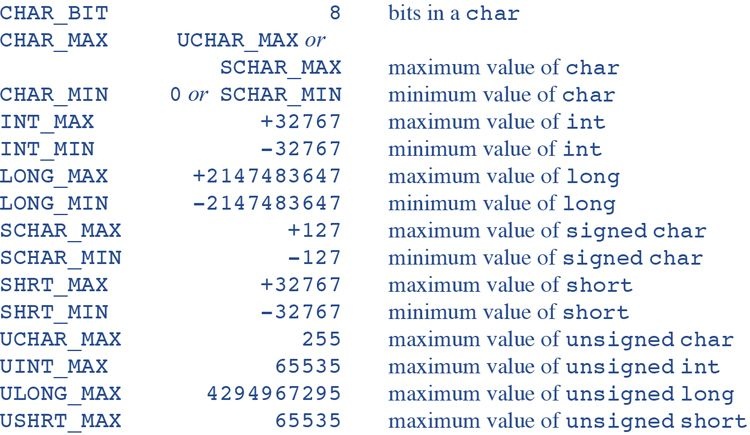
In Appendix B, there are two charts that list all the constants defined
in <limits.h> and <float.h>.

We can include the two header files and print the value of the constants we need to know.
#include <stdio.h>
#include <limits.h>
#include <float.h>
main()
{
printf("signed char: %d to %d\n", SCHAR_MIN, SCHAR_MAX);
printf("unsigned char: 0 to %d\n", UCHAR_MAX);
printf("signed int: %d to %d\n", INT_MIN, INT_MAX);
printf("unsigned int: 0 to %u\n", UINT_MAX);
printf("signed short: %d to %d\n", SHRT_MIN, SHRT_MAX);
printf("unsigned short: 0 to %d\n", USHRT_MAX);
printf("signed long: %ld to %ld\n", LONG_MIN, LONG_MAX);
printf("unsigned long: 0 to %lu\n", ULONG_MAX);
printf("float: %g to %g\n", FLT_MIN, FLT_MAX);
printf("double: %g to %g\n", DBL_MIN, DBL_MAX);
}Note: these constants are implementation-defined and considering this book was written when 32-bit machines prevailed, you will likely find that some of the limits differ from what is listed in the charts.
Note: in the code above, we also see some new format specifiers:
%u, %ld, %lu, and
%g. The first is used for unsigned integers
and the specifiers with l correspond to the long types.
Perhaps the most interesting of these is %g; it works with
both float and double literals and displays
them in scientific notation. See
this page
for the full list of valid format specifiers.
Note: the limits for the floating-point minimums
(FLT_MIN and DBL_MIN) are not set to the
actual minimum value of the type, but rather the smallest positive
normalized value (we will look into what that word means soon.)
Let us now look at how we can compute the limits. This exercise alongside many to come leave lots of room for interpretation. What does it mean to compute a limit? Here, we look at two ways.
The first method revolves around the idea that after a variable reaches
its limit, attempting to increment its value would result in the
incorrect value. We create a temp variable alongside two
other variables to store the minimum and maximum values. In order to
calculate the maximum value, we set temp to one and
max to zero to start. We then enter a for-loop
that increments both values every iteration and runs as long as
temp is one more than max (i.e. as long as the
behavior is as expected). We do the same thing to calculate
min, except temp will always be one less and both
values will decrement every iteration instead.
#include <stdio.h>
main()
{
signed char min, max, temp;
unsigned char umax;
min = max = 0;
for (temp = -1; temp == min - 1; --temp)
--min;
for (temp = 1; temp == max + 1; ++temp)
++max;
for (temp = 1; temp == umax + 1; ++temp)
++umax;
printf("signed char: %d to %d\n", min, max);
printf("unsigned char: 0 to %d\n", umax);
/* the rest of the limits are computed the same way */
}
Although all the limits are implementation-defined, most
implementations will have signed chars ranging from -128
to 127 and unsigned chars ranging from 0 to 255. This is
because a char usually takes up a byte, or eight bits in
memory. 1111 1111binary translates to 255, the maximum value
of an unsigned char. As for signed chars, in
a two's complement machine (which is most machines these days), the
leftmost bit has the place value -128 in order to also allow negative
values. Thus, 1000 0000 (-12810) and 0111 1111
(12710) correspond to the limits of a
signed char. Perhaps we can use this information to find
another way to calculate the limits.
The method we had previously used works, but it would take an
unfathomably long time to calculate the limits of longer types, such as
unsigned long. Knowing that values are stored as bits
under the hood, a more informed approach would be to multiply by two
every iteration instead. We can employ a similar tactic from before
where we create two variables, multiply one first, and assign its value
to the other as long as it is still within the range. This continues
until the variable goes out of the range. If max and
temp are unsigned chars, by the end,
max will be equal to 128, or 1000 0000binary. The
negative of max is the minimum value for a
signed char, one less is the maximum value, and
max + (max - 1) (i.e. 1000 0000binary + 0111
1111binary) is the maximum value for an
unsigned char. The same logic applies to the other types.
#include <stdio.h>
main()
{
unsigned char max, temp;
temp = 2;
for (max = 1; max == temp / 2; temp = temp * 2)
max = c;
printf("signed char: %d to %d\n", -max, max - 1);
max = max + (max - 1);
printf("unsigned char: 0 to %d\n", max);
/* the rest of the limits are computed the same way */
}
Note: we check if max == temp / 2 instead of
temp == max * 2 because when max reaches the
maximum value, multiplying it by two would give us the wrong value.
Note: we write max + (max - 1) instead of
max * 2 - 1 because the value of max * 2
exceeds the maximum value for a unsigned char.
You might have realized that the approach we have used here does not work with the floating-point types. This is because they are stored in a different way. To be able to calculate their limits, we first need to take a look at how floating-point numbers work.
Floating-point is analogous to scientific notation, but it uses binary instead. Almost all implementations of floating-point numbers use the standard IEEE 754, which states that the bits allocated to a floating-point number are split into three parts: the sign bit, the exponent, and the fraction. The sign bit comes first and it determines if the number is positive or negative. The exponent is the power of two the number is multiplied by, similar to how numbers are multiplied by powers of ten in scientific notation. In a 32-bit floating-point number, eight bits are allocated to the exponent, so its value is shifted by -127 in order to also allow negative exponents. This means 1000 0000 represents one, not 128. Finally, the fraction is the part that contains the digits of the number using binary place values (e.g. 1/2, 1/4, 1/8, etc.) In scientific notation, the first digit of the fraction must be nonzero, and in binary, there is only one nonzero digit: one, so it is implied and not included in the bits for the fraction. Here are a few examples of the bit representations for various floating-point values.
| Floating-point (32-bit) | Translation |
|---|---|
| 0 10000000 01000000000000000000000 | 1.25 * 21 |
| 1 10000010 10000000000000000000000 | -1.5 * 23 |
| 0 01111101 11000000000000000000000 | 1.75 * 2-2 |
Note: Floating-point values tend to be inaccurate. For example, 0.1 is stored as 0.100000001490116119384765625 because a tenth in binary is 0.1001... and there are not an infinite number of bits to store the value. To account for this, past a certain threshold the number gets rounded. This page has more details about rounding errors.
Note: When the exponent is set to all zeros (equivalent to -127
in a 32-bit floating-point number), the number becomes denormalized.
This means that the leading one for the fraction is no longer implied.
This allows for very small values to be stored at the expense of
accuracy. As mentioned previously, the constants FLT_MIN
and DBL_MIN are equal to the smallest
normalized values, and that is what we will be
calculating for as well.
With this in mind, the largest normalized value for a
float is the fraction 2.0 times the largest exponent, and
the smallest normalized value is the fraction 1.0 divided by one less
than the largest exponent. We can calculate the exponent in the same
way we calculated the limits for the integer types.
#include <stdio.h>
main()
{
float exponent, temp;
temp = 2.0;
for (exponent = 1.0; exponent == temp / 2.0; temp = temp * 2.0)
exponent = f;
printf("float: %g to %g\n", 1.0 / (exponent / 2.0), 2.0 * exponent);
}Note: in case it was unclear, multiplying exponent by two is the equivalent of doubling the exponent part of its bit representation whilst leaving the fraction part as 1.0.
Note: In order for this to work with double, for
the maximum, we multiply exponent by 1.999999999999999
instead of 2.0 in order to avoid the number rounding to Infinity.
Calculating floating-point limits is extremely finicky and so
1.999999999999999 may not work on all implementations. You can play
around with this yourself to find out at what value the number rounds
up for you. If you ever need to use the limits in one of your programs
(especially for a floating-point value), there is a reason why
pre-defined constants exist!